Academic Year 2020-2021

Christoph Thäle (Ruhr Universität Bochum), Poisson hyperplanes in hyperbolic space

Abstract: In the focus of this talk are random tessellations in hyperbolic space induced by Poisson point processes on the space of hyperbolic hyperplanes (totally geodesic subspaces of co-dimension 1). In the first part of the talk we consider the so-called k-skeleton of such tessellations and prove that, when observed in a sequence of increasing observation windows, the k-volume of the k-skeleton satisfies a central limit theorem only for dimensions 2 and 3 and that asymptotic normality fails in all higher dimensions. We indicate possible generalizations to Poisson processes of lower-dimensional random subspaces as well. If time permits we also describe a way to address the combinatorial structure of the zero cell of a hyperbolic hyperplane tessellation. In particular we present a fully explicit formula for the number of facets of this cell.

Maurizia Rossi (University of Milano-Bicocca), Non-universal fluctuations of the empirical measure for sphere-cross-time random fields

Abstract: In this talk we consider isotropic and stationary real Gaussian sphere-cross-time random fields and we investigate the large time asymptotic behavior of the empirical measure at any threshold, covering both cases when the field exhibits short and long memory, i.e. integrable and non-integrable temporal covariance. It turns out that the limiting distribution is not universal, depending both on the memory parameters and the threshold. In particular, in the long memory case a form of Berry’s cancellation phenomenon occurs at zero-level, inducing phase transitions for both variance rates and limiting laws. (This talk is based on a joint work with D. Marinucci and A. Vidotto.)

Yvik Swan (Université libre de Bruxelles),  Stein’s density method for multivariate continuous distributions

Slides Video (Password: hXPJCnD5)

Abstract: We will discuss a general framework for Stein’s density method for multivariate continuous distributions. The approach associates to any probability density function a canonical operator and Stein class, as well as an infinite collection of operators and classes which we call standardizations. These in turn spawn an entire family of Stein identities and characterizations for any continuous distribution on Rd, among which we highlight those based on the score function and the Stein kernel. A feature of these operators is that they do not depend on normalizing constants. A new definition of Stein kernel is introduced and examined; integral formulas are obtained through a connection with mass transport, as well as ready-to-use explicit formulas for elliptical distributions. The flexibility of the kernels is used to compare in Stein discrepancy (and therefore 2-Wasserstein distance) between two normal distributions, Student and normal distributions, as well as two normal-gamma distributions. Upper and lower bounds on the 1-Wasserstein distance between continuous distributions are provided, and computed for a variety of examples: comparison between different normal distri- butions (improving on existing bounds in some regimes), posterior distributions with different priors in a Bayesian setting (including logistic regression), centred Azzalini- Dalla Valle distributions. Finally the notion of weak Stein equation and weak Stein factors is introduced, and new bounds are obtained for Lipschitz test functions if the distribution admits a Poincaré constant, which we use to compare in 1-Wasserstein distance between different copulas on the unit square. (arXiv : https://arxiv.org/abs/2101.05079)

Louis Gass (IRMAR), A Salem Zygmund approach to almost sure asymptotics concerning the nodal measure of Riemannian random waves

Video (Password: TknKfmQ4)

Abstract: Let 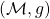be a compact, boundaryless Riemannian manifold, and 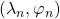the sequences of (ordered) Laplace eigenvalues and eigenfunctions, satysfying 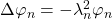. We consider the model of Riemannian random waves defined by 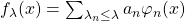, where 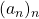is a iid sequence of Gaussian random variables. With probability one with respect to the Gaussian coefficients, we establish that the process 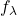, properly rescaled and evaluated at an independently and uniformly chosen point X on the manifold, converges in distribution towards an universal Gaussian field as 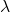grows to infinity. Using the continuity of the nodal measure with respect to the 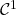topology, we deduce that almost surely with respect to the Gaussian coefficient, the nodal measure of 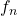weakly converges towards the Riemannian volume.

Anna Gusakova (Ruhr-Universität Bochum), Random simplicial tessellations: high-dimensional probabilistic behaviour of the typical cells

Video (Password: 3iDKQ6fn)

Abstract: A tessellation in 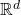is a locally finite collection of convex polytopes, which cover the space and have disjoin interior. In this talk we consider a few models of random simplicial tessellations, the so-called Delaunay tessellations, whose construction is based on Poisson point process. Among them is the classical Poisson-Delaunay tessellation.
The main object we are interested in is the typical cell of a random tessellation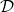 . Intuitively, one can think of it as a randomly chosen polytope from the collection 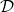, assuming that each polytope has the same chance to be chosen. Considering the volume of the typical cells of our models we derive the explicit formulas for the moments as well as probabilistic representation in term of independent gamma- and beta-distributed random variables. Moreover, we investigate the limiting probabilistic behaviour of the logarithmic volume of typical cell, when dimension 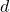tends to infinity. In particular we establish central limit theorem and large deviation principle.

Hugo Vanneuville (Université Grenoble-Alpes), The percolation phase transition of the random plane wave

Video (Password: 7Bj6bgc6)

Abstract: Consider the random plane wave 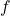, which is a random eigenfunction of the Laplacian in 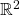. Given a real number 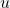, we study the connectivity properties of the set , and we show that the model undergoes a percolation phase transition at 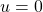: if 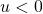then a.s. there is no unbounded connected component in while this is a.s. the case if 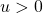. As I will explain in the talk, the main difficulty is that the field is not positively correlated. In the talk, I will present the strategy of proof, based on some superconcentration considerations that have enabled us to revisit the following general idea from (Russo, 1982; Talagrand, 1994…): “an event satisfies a phase transition if it depends little on any given point”. This is joint work with Stephen Muirhead and Alejandro Rivera.

Vytauté Pilipauskaite (University of Luxembourg), Local scaling limits of Lévy driven fractional random fields

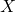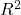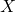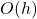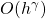Abstract: We obtain all local scaling limits for a class of Lévy driven fractional random fields on . More specifically, the random field is defined as integral of a non-random function with respect to infinitely divisible random measure. The scaling procedure involves increments of X over points between which the distance in the horizontal and vertical directions shrinks respectively as and as 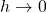for a given 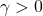. We consider two types of increments of 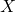: usual increment and rectangular increment. We call their local scaling limits respectively 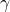-tangent and 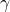-rectangent random fields. We show that for above 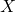both types of local scaling limits exist for any 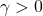and undergo a transition at some 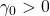. We also discuss properties of these limits. This is a joint work with Donatas Surgailis (Vilnius University, Lithuania).

Etienne Roquain (LPSM), False Discovery Rate control with unknown null distribution

Abstract: Classical multiple testing theory prescribes the null distribution, which is often a too stringent assumption for nowadays large scale experiments. This paper presents theoretical foundations to understand the limitations caused by ignoring the null distribution, and how it can be properly learned from the (same) data-set, when possible. While an oracle procedure in that case is the Benjamini Hochberg procedure applied with the true (unknown) null distribution, we pursue the aim of building a procedure that asymptotically mimics the performance of the oracle (AMO in short). For a Gaussian null, our main result states that an AMO procedure exists if and only if the sparsity parameter k (number of false nulls) is of order less than 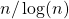, where n is the total number of tests.
This is a joint work with Nicolas Verzelen, https://arxiv.org/abs/1912.03109.

Chiara Amorino (University of Luxembourg), Rate of estimation for the stationary distribution of jump-processes over anisotropic Holder classes

Abstract: We consider the solution 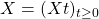of a multivariate stochastic differential equation with Levy-type jumps and with unique invariant probability measure
with density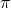 . We assume that a continuous record of observations 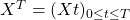is available.
In the case without jumps, under respectively isotropic and anisotropic Holder smoothness constraints, Dalalyan and Reiss [1] and Strauch [2] have found convergence rates of invariant density estimators which are considerably faster than those known from standard multivariate density estimation.
We extend the previous works by obtaining, in presence of jumps and in an anisotropic context, some estimators which achieve the continuous convergence rates in mono and bi-dimensional cases and a convergence rate faster than the ones found by Strauch [2] for .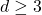
Moreover, we obtain a minimax lower bound on the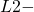 risk for pointwise estimation, with the same rate up to a 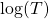term. It implies that, on a class of diffusions whose invariant density belongs to the anisotropic Holder class we are considering, it is impossible to find an estimator with a rate of estimation faster than the one we propose.
References
[1] Dalalyan, A. and Reiss, M. (2007). Asymptotic statistical equivalence for ergodic diffusions: the multidimensional case. Probab. Theory Relat. Fields, 137(1), 25-47.
[2] Strauch, C. (2018). Adaptive invariant density estimation for ergodic diffusions over anisotropic classes. The Annals of Statistics, 46(6B), 3451-3480. 1

Richard Samworth (University of Cambridge), USP: an independence test that improves on Pearson’s chi-squared and the 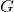-test

Abstract: We introduce the U-Statistic Permutation (USP) test of independence in the context of discrete data displayed in a contingency table. Either Pearson’s chi-squared test of independence, or the Generalised Likelihood Ratio test (G-test), are typically used for this task, but we argue that these tests have serious deficiencies, both in terms of their inability to control the size of the test, and their power properties. By contrast, the USP test is guaranteed to control the size of the test at the nominal level for all sample sizes, has no issues with small (or zero) cell counts, and is able to detect distributions that violate independence in only a minimal way. The test statistic is derived from a U-statistic estimator of a natural population measure of dependence, and we prove that this is the unique minimum variance unbiased estimator of this population quantity.
In the last one-third of the talk, I will show how this is a special case of a much more general methodology and theory for independence testing.

Hélène Halconruy (Télécom ParisTech), Kernel selection in nonparametric regression

Abstract: Adaptative estimation has become a key issue in nonparametric estimation and has been widely investigated for years. Several data-driven procedures were designed to achieve the flexible selection of a performing estimator from a collection of preliminary ones. Among them, the Goldenshluger-Lepski’s method (2011) provides a bandwidth selection procedure for kernel estimators that reaches the bias-variance compromise. However, its difficult implementation led C. Lacour, P. Massart and V. Rivoirard (2017) to introduce the so-called Penalized Cross Overfitting (PCO) estimator based on the concept of minimal penalty. In a joint work with Nicolas Marie, we investigate a regression model for which we select via the PCO method an estimator of 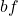( 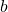is the regression function, 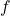the density of the input variable) and prove an oracle inequality for the associated adaptative estimator. Within this broad framework, our result generally performs. It enables to cover the well-known bandwidth selection for kernel-based estimators and to extend the method to the dimension selection for anisotropic projection estimators.

Xiaochuan Yang (University of Bath.), Quantitative two-scale stabilisation on the Poisson space

Abstract: Stabilisation theory was initiated in the early 2000 by Penrose and Yukich as a kind of high level abstraction of the famous CLT for minimal spanning trees of Kesten and Lee. Since its birth, this beautiful theory constitutes one of the most fundamental ideas for proving Gaussian approximation of stochastic geometric models, e.g. coverage processes, random tessellations, spatial networks etc. In a recent joint work with G. Peccati and R. Lachieze-Rey, we develop a quantitative stabilization theory which gives rates of multivariate Gaussian approximation for general stabilizing Poisson functionals, extending some estimates from a recent paper of Chatterjee and Sen on the rate of normal convergence of minimal spanning trees. Several examples are worked out to illustrate our results, including the online nearest neighbor graphs, edge statistics of Euclidean minimal spanning trees, and excursion of heavy tailed shot noise random fields.

James Thompson (University of Luxembourg.), An Agent-Based Model of COVID-19

Video (Password: eQFmxaD6) Slides

Abstract: The ongoing coronavirus pandemic is the most disruptive event in recent history. It is of vital importance that we continue to build a rigorous understanding of how the SARS-CoV-2 virus spreads within the human population, and predict the impact of interventions. Our team has approached this problem by developing a detailed agent-based model of COVID-19, offering unique insights into the dynamics and control of the disease. While we have focused on simulating the epidemic in Luxembourg, the model has been constructed in such a way that it can also be applied to other regions. This project is a joint work with Stephen Wattam and Mikolaj Kasprzak, and is currently a work in progress.

Martin Wahl (Humboldt-Universität zu Berlin), Upper and lower bounds for the estimation of principal components

Abstract: In settings where the number of observations is comparable to the dimension, principal component analysis (PCA) reveals some unexpected phenomena, ranging from eigenprojector inconsistency to eigenvalue upward bias. While such high-dimensional phenomena are now well understood in the spiked covariance model, the goal of this talk is to discuss some extensions for the case of PCA in infinite dimensions. In such scenarios the spiked covariance model becomes less important and typically different eigenvalue decay assumptions are investigated instead. Our main results show that the behavior of eigenvalues and eigenprojectors of empirical covariance operators can be characterized by the so-called “relative ranks”. The proofs rely on a novel perturbation-theoretic framework, combined with concentration inequalities for sub-Gaussian chaoses in Banach spaces. If time permits, we will also present corresponding minimax lower bounds for the estimation of eigenprojectors. These are obtained by a van Trees (resp. Cramér-Rao) inequality for invariant statistical models.

Lutz Dümbgen (University of Bern), Shape-Constrained Distributional Regression – Stochastic and Likelihood Ratio Order

Abstract: We consider nonparametric bivariate regression with generic observations (X,Y). A possible and often natural assumption is that the conditional distribution of Y, given that X = x, is “increasing” in x. A standard notion of “increasing” would be the usual stochastic order, and we present estimators and asymptotic properties for that setting. A stronger notion of order is the likelihood ratio order which is well-known from mathematical statistics and binary classification. We review this property briefly but in full generality and describe its relation to so-called multivariate total positivity of order 2 (MTP2). Then we present an algorithm to estimate the joint distribution of (X,Y) from empirical data under the sole assumption that the conditional distribution of Y, given that X = x, is increasing in x with respect to likelihood ratio order. This is joint work with Alexandre Mösching (Bern, Göttingen).

Ismael Castillo (LPSM), Supremum-norm inference with Bayesian CART

Abstract: This paper affords new insights about Bayesian CART in the context of structured wavelet shrinkage. We show that practically used Bayesian CART priors lead to adaptive rate-minimax posterior concentration in the supremum norm in Gaussian white noise, performing optimally up to a logarithmic factor. To further explore the benefits of structured shrinkage, we propose the g-prior for trees, which departs from the typical wavelet product priors by harnessing correlation induced by the tree topology. Building on supremum norm adaptation, an adaptive non-parametric Bernstein-von Mises theorem for Bayesian CART is derived using multiscale techniques. For the fundamental goal of uncertainty quantification, we construct adaptive confidence bands with uniform coverage for the regression function under self-similarity. This is joint work with Veronika Rockova (Chicago)

Emmanuel Rio (University of Versailles), About the constants in the deviation inequalities for martingales

Abstract: In this talk, we will give deviations inequalities for martingales or sums of independent random variables. We will start by giving some constants in Fuk-Nagaev type inequalities. Next we will give an other approach, which allows to give more precise results in the case of martingales with finite third moments. Finally we apply estimates of the minimal distances in the central limit theorem to get upper bounds for the tail-quantiles of sums of independent random variables.

Gérard Biau (Sorbonne Université), Theoretical Insights into Wasserstein GANs

Abstract: Generative Adversarial Networks (GANs) have been successful in producing outstanding results in areas as diverse as image, video, and text generation. Building on these successes, a large number of empirical studies have validated the benefits of the cousin approach called Wasserstein GANs (WGANs), which brings stabilization in the training process. In the present contribution, we add a new stone to the edifice by proposing some theoretical advances in the properties of WGANs. First, we properly define the architecture of WGANs in the context of integral probability metrics parameterized by neural networks and highlight some of their basic mathematical features. We stress in particular interesting optimization properties arising from the use of a parametric 1-Lipschitz discriminator. Then, in a statistically-driven approach, we study the convergence of empirical WGANs as the sample size tends to infinity, and clarify the adversarial effects of the generator and the discriminator by underlining some trade-off properties. These features are finally illustrated with experiments using both synthetic and real-world datasets.

Vincent Rivoirard (CEREMADE, Université Paris Dauphine), Nonparametric inference for Hawkes processes

Abstract: Hawkes processes are widely applied to event-type data with complex dependencies on the past of the process. They are particularly used in seismology, neuroscience, genetics and social network analysis. The goal of this talk is to present recent advances for nonparametric inference for multivariate Hawkes processes. In the fist part of this talk, frequentist estimation of Hawkes parameters by using Lasso-type estimators is described. Then, the Bayesian setting is considered. Concentration rates for the posterior distribution under reasonable assumptions on the prior distribution are established, first for linear multivariate Hawkes models, then for nonlinear ones. We also present a simulation study to illustrate our results and to study empirically the inference on functional connectivity graphs of neurons.

Olivier Lopez (Sorbonne Université), Generalized Pareto regression trees applied to cyber-risk analysis

Abstract: With the rise of the cyber insurance market, there is a need for better quantification of the economic impact of this risk and its rapid evolution. Due to the relatively poor quality and consistency of databases on cyber events, and because of the heterogeneity of cyber claims, evaluating the appropriate premium and/or the required amount of reserves is a difficult task. In this paper, we propose a method based on regression trees to analyze cyber claims to identify criteria for claim classification and evaluation. We particularly focus on severe/extreme claims, by combining a Generalized Pareto modeling—legitimate from Extreme Value Theory—and a regression tree approach. Combined with an evaluation of the frequency, our procedure allows computations of central scenarios and extreme loss quantiles for a cyber portfolio. Finally, the method is illustrated on a public database

Michel Denuit (Université catholique de Louvain), Risk reduction by conditional mean risk sharing

Abstract: This talk considers the conditional mean risk allocation for independent but heterogeneous losses that are gathered in an insurance pool, as defined by Denuit and Dhaene (2012, Insurance: Mathematics and Economics). The behavior of individual contributions to total losses is studied when the number of participants to the pool increases. It is shown that enlarging the pool is generally beneficial and that there exists a critical number of participants such that collaborative insurance outperforms commercial one. The linear fair risk allocation approximating the conditional mean risk sharing rule is identified, providing practitioners with a useful simplification applicable within large pools.
This talk is based on several papers co-authored with Christian Robert from the Laboratory in Finance and Insurance (LFA), CREST, ENSAE, Paris.