Academic Year 2019-2020
- Home >
- Academic Year 2019-2020
- Wednesday 01.07.2020, 3pm, Webex
Francesco Grotto (SNS, Pisa), Invariant Measures for 2d Incompressible Fluid Dynamics Models
Abstract: The Hamiltonian structure of 2d Euler’s equations and its variants allows the formal derivation of invariant measures from conservation laws. Gaussian and Poissonian invariant measures thus obtained pose nontrivial questions, concerning the singular dynamics they induce and the relations between their very different natures. We will give an overview of classical and more recent results on the topic.
- Thursday 14.05.2020, 5pm, Webex
Fei Pu (University of Luxembourg), Spatial limit theorems for stochastic heat equation via Poincare inequality
Abstract: In this talk, I will present spatial limit theorems for the solution to stochastic heat equations, which include ergodicity, central limit theorem and Poisson limit theorem. The tool to study these properties is Malliavin calculus, in particular, the Poincare inequality.
- Friday 20.03.2020, 10am, Webex
Arturo Jaramillo (University of Luxembourg), Quantitative Erdös-Kac theorem for additive functions, a self-contained probabilistic approach
Abstract: The talk will have as starting point the classical Erdös-Kac theorem, a result of great importance in probabilistic number theory, which states that the fluctuations of the standardized number of distinct primes of a uniformly chosen number between one and n, are asymptotically Gaussian. Naturally, after the publication of this result, a quantitative version of it was explored by many authors. LeVeque conjectured that the optimal rate of convergence (in the topology of Kolmogorov distance) was of the order
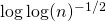 . This was subsequently proved by Turan and Rényi by means of a very clever manipulation of the associated characteristic function. Unfortunately, up to this day, all of the approaches for solving LeVeque’s conjecture(in its full generality) rely on highly non-trivial complex analysis tools, whereas the purely probabilistic tools have only been successfully applied for obtaining non-optimal assessments of the aforementioned rate.
. This was subsequently proved by Turan and Rényi by means of a very clever manipulation of the associated characteristic function. Unfortunately, up to this day, all of the approaches for solving LeVeque’s conjecture(in its full generality) rely on highly non-trivial complex analysis tools, whereas the purely probabilistic tools have only been successfully applied for obtaining non-optimal assessments of the aforementioned rate.
In this talk, we present a new perspective to estimate the distance to a Gaussian distribution (with respect to Kolmogorov and Wasserstein metric), for general additive functions applied to a uniformly chosen number between one and n . Our approach is probabilistic and does not rely on prior knowledge of the underlying characteristic function. Our main result is an optimal Berry-Esseen type bound in the Kolmogorov distance and the Wasserstein distance. In the special case where the additive function is taken to be the prime factors counting function (with and without accounting of multiplicities), we also show Poisson approximations with optimal error bounds in the total variational distance. - Thursday 12.03.2020, 2pm, MNO 5A
Cecile Durot (Université Paris Nanterre), Divide and Conquer methods in monotone regression
Abstract: The divide and conquer principle in studied in the isotonic regression problem, where rates of convergence are slower than the square-root of the sample size, and limit distributions are non-Gaussian. For a fixed model, the pooled estimator obtained by averaging non-standard estimates across mutually exclusive subsamples, outperforms the non-standard monotonicity-constrained (global) estimator based on the entire sample in the sense of point wise estimation. However, this gain in efficiency under a fixed model comes at a price: the pooled estimator’s performance, in a uniform sense over a class of models worsens as the number of subsamples increases, leading to a version of the super-efficiency phenomenon. Then, we build a corrected pooled estimator that does not suffer from the super-efficiency phenomenon and allows for some heterogeneity in data. The new estimator essentially reverses the steps involved in constructing the above pooled estimator: we first smooth (by local averaging) on each subsample, and then isotonize the pooled smoothed data. Joint work with Moulinath Banerjee and Bodhisattva Sen.
- Friday 06.03.2020, 10:30am, MNO 5A
Vlad Margarint (NYU Shanghai), Backward Loewner Differential Equation as a Singular Rough Differential Equation, the welding homeomorphism and new structural information about the SLE traces
Abstract: In this talk, I will give an overview of the Schramm-Loewner Evolutions (SLE) theory and present new results on this theory based on the analysis of a Singular Differential Equation that appears naturally in this context. This equation appears when extending the conformal maps to the boundary and can be thought of as a singular Rough Differential Equation (RDE), as in Rough Path Theory. In the study of RDEs, questions such as continuity of the solutions, the uniqueness/non-uniqueness of solutions depending on the behavior of parameters of the equation, appear naturally. We adapt these type of questions to the study of the backward Loewner differential equation in the upper half-plane, and the conformal welding homeomorphism. This view will allow us to obtain some new structural and geometric information about the SLE traces in the regime where they have double points.
This first part is a joint work with Dmitry Belyaev and Terry Lyons.
In the second part, I plan to cover the main ideas of an independent project that uses ideas from Quasi-Sure Stochastic Analysis through Aggregation in order to study SLE theory quasi-surely. This quasi-sure study will allow us to overcome some of the difficulties with the previous analysis that I will emphasize throughout the talk. - Thursday 05.03.2020, 1pm, MNO 5A
Benjamin Arras (Université de Lille), From generalized Mehler semigroups to stability results for Poincaré-type inequalities
Abstract: In this talk, I will present some recent results around Stein’s method for multivariate stable laws and generalized Mehler semigroup. This is based on joint works with Christian Houdré (GaTech).
- Monday 2.03.2020, 2pm-2:45pm, MNO 5A
Guenter Last (Karlsruhe Institute of Technology), Unbiased embedding of excursions into Brownian motion
Abstract: : In this talk, we discuss an embedding problem for a two-sided Brownian motion. We consider an excursion event
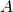 with positive and finite Itô-measure and construct a stopping time
with positive and finite Itô-measure and construct a stopping time 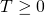 such the two-sided Brownian motion centered around
such the two-sided Brownian motion centered around 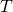 splits into three independent pieces: a time reflected Brownian motion on
splits into three independent pieces: a time reflected Brownian motion on ![Rendered by QuickLaTeX.com (-\infty,0]](https://probstat-seminar.uni.lu/wp-content/ql-cache/quicklatex.com-6e4b814362484fd2b1214984728b3036_l3.png) , an excursion distributed according to a conditional Itô law (given
, an excursion distributed according to a conditional Itô law (given 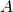 ) and a Brownian motion starting after this excursion. The proof relies on Palm theory for random measures and on excursion theory. Therefore we shall begin with a short review of some fundamental facts on invariant balancing transports of random measures. This talk is based on joint work with Wenpin Tang and Hermann Thorisson.
) and a Brownian motion starting after this excursion. The proof relies on Palm theory for random measures and on excursion theory. Therefore we shall begin with a short review of some fundamental facts on invariant balancing transports of random measures. This talk is based on joint work with Wenpin Tang and Hermann Thorisson. - Monday 2.03.2020, 2:50pm-3:35pm, MNO 5A
D. Yogeshwaran (ISI, Bangalore), Random minimal spanning acycles.
Abstract: It is well-known that extremal edge-weights on a minimal spanning tree, nearest-neighbour distances and connectivity threshold are inter-related for randomly weighted graphs. In this talk, we shall look at generalization of this result to randomly weighted simplicial complexes. The first part of the talk shall be about defining spanning acycles and establishing it to be a natural topological generalisation of spanning trees. We shall give the Kruskal’s algorithm to generate minimal spanning acycles. As a consequence of the Kruskal’s algorithm, we shall obtain a connection between minimal spanning acycles and persistent homology. We shall explore applications of these results in the context of random d-complexes and in particular, paying attention to extremal face-weights of the minimal spanning acycles on a complete d-complex with i.i.d. face weights. This is a joint work with Primoz Skraba and Gugan Thoppe. Time permitting, I will sketch some on-going work with Primoz Skraba on Euclidean minimal spanning acycles.
- Thursday 13.02.2020, 2pm, MNO 5A Guillaume Maillard (Université Paris-Sud), Aggregated hold-out Abstract: Aggregated hold-out (Agghoo) is a hyperparameter aggregation method which averages learning rules selected by hold-out (i.e cross-validation with 1 split). Theoretical guarantees on Agghoo ensure that one can use it safely: for a convex risk, at worse, Agghoo performs like the hold-out. For the hold-out, oracle inequalities are known for bounded losses, as in binary classification. We show that classical methods can be extended, under appropriate assumptions, to some unbounded risk-minimization problems. In particular, we obtain an oracle inequality in sparse linear regression with Huber loss, without requiring the
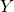 variable to be bounded or using truncation. To further investigate the effects of aggregation on performance, we conduct some numerical experiments. They show that aggregation brings a significant improvement over the hold-out. Compared to cross-validation, Agghoo appears to perform better when the intrinsic dimension is sufficiently high, and when there are correlations between predictive and noise covariates.
variable to be bounded or using truncation. To further investigate the effects of aggregation on performance, we conduct some numerical experiments. They show that aggregation brings a significant improvement over the hold-out. Compared to cross-validation, Agghoo appears to perform better when the intrinsic dimension is sufficiently high, and when there are correlations between predictive and noise covariates.
- Thursday 06.02.2020, 2pm, MNO 5A Richard Nickl (University of Cambridge), On Bayesian solutions of some statistical inverse boundary value problems Abstract: We discuss Bayesian inference in a class of statistical non-linear inverse problems arising with partial differential equations (PDEs): The main mathematical idea behind non-invasive tomography methods is related to the fact that observations of boundary values of the solutions of certain PDEs can in certain cases determine the parameters governing the dynamics of the PDE also in the interior of the domain in question. The parameter to data maps in such settings are typically non-linear, as with the Calderon problem (relevant in electric impedance tomography) or with non-Abelian X-ray transforms (relevant in neutron spin tomography). Real world discrete data in such settings carries statistical noise, and Bayesian inversion methodology has been extremely popular in computational and applied mathematics in the last decade after seminal contributions by Andrew Stuart (2010) and others. In this talk we will discuss recent progress which provides rigorous statistical guarantees for such inversion algorithms in the large sample/small noise limit.
- Friday, 31.01.2020, 10:35am, MNO 5A Xiao Fang (The Chinese University of Hong Kong), Wasserstein-2 bounds in normal approximations under local dependence with applications to strong embeddings Abstract: We obtain a general bound for the Wasserstein-2 distance in normal approximation for sums of locally dependent random variables. The proof is based on an asymptotic expansion for expectations of second-order differentiable functions of the sum. We apply the main result to obtain Wasserstein-2 bounds in normal approximation for sums of
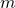 -dependent random variables, U-statistics and subgraph counts in the Erdös-Rényi random graph. We also discuss an application to strong embeddings.
-dependent random variables, U-statistics and subgraph counts in the Erdös-Rényi random graph. We also discuss an application to strong embeddings.
- Thursday 30.01.2020, 2pm, MNO 5A Alexandre Moesching (University of Bern), Order Constraints in Nonparametric Regression Abstract: Imposing a nonparametric qualitative constraint in a statistical model has shown its benefit on several occasions, for example in circumstances where a parametric model is hard to justify but a qualitative constraint on the distribution is natural. We consider a stochastic ordering constraints on an unknown family of distributions
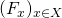 , with a fixed subset
, with a fixed subset 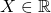 , and discuss nonparametric estimation procedures based on a sample
, and discuss nonparametric estimation procedures based on a sample 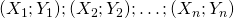 such that, conditional on the
such that, conditional on the 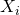 the
the 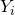 are independent random variables with distribution functions
are independent random variables with distribution functions 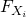 .
.
