Academic Year 2021-2022

Abstract: We present some Poisson process approximation results for stabilizing functionals of Poisson (or Binomial) processes that arise in stochastic geometry. Our bounds are derived for the Kantorovich-Rubinstein distance between a point process and an appropriate Poisson point process. We will discuss application to largest k-nearest neighbour distances. This is based on a joint project with Omer Bobrowski (Technion) and Matthias Schulte (Hamburg Institute of Technology) [see arXiv:2104.13261].

Abstract: In this talk, we introduce a new approach, called Isolate-Detect (ID), for the consistent estimation of the number and location of multiple generalized change-points in noisy data sequences. Examples of signal changes that ID can deal with are changes in the mean of a piecewise-constant signal and changes, continuous or not, in the linear trend. The number of change-points can increase with the sample size. The proposed method is based on an isolation technique, which prevents the consideration of intervals that contain more than one change-point. This isolation enhances ID’s accuracy as it allows for detection in the presence of frequent changes of possibly small magnitudes. In the end, we provide a general method with very good practical performance and minimal parameter choice. ID turns out to be at least as accurate as the state-of-the-art methods; most of the times it significantly outperforms them. ID is implemented in the R packages IDetect and breakfast, available from CRAN.

Abstract: The last two decades have seen the emergence of a new area of probability theory concerned with random fractal structures characterized by a certain invariance under conformal (angle-preserving) transformations. These structures often emerge when taking the continuum scaling limit of two-dimensional models of statistical mechanics with parameters chosen at or near those values where a continuous phase transition occurs. The study of such structures has had deep repercussions on both mathematics and physics, generating tremendous progress in areas ranging from probability theory to statistical mechanics to conformal field theory. In this talk, I will give a personal perspective on some aspects of this new area of probability theory, focusing for concreteness on two specific examples, the Ising model and percolation.

Abstract: We will talk about some pathwise properties of the planar Brownian motion, related to its winding around deterministic and random points. This will allow to state a Green formula, which describes Stratonovich integrals as areas enclosed by the path. Then, we will consider the average winding around the points of a Poisson process with large intensity. In this model motivated by the  physics of an electron moving inside a crystal, the law of large numbers fails and must be replaced with a 1-stable CLT. By endowing the Brownian motion with a random non-continuous rough path extension, we will describe the physical effects of the Poisson impurities in the crystal as rough path integrals along the path.

Abstract: In this talk, focused on free probability, we will define respectively the semicircular distribution and Wigner chaos which are respectively the free analogues of the gaussian random variable and Wiener chaos. Firstly, we will discuss how non-commutative stochastic calculus and Free Malliavin calculus invented by Biane and Speicher in 1998 has allowed several authors to contribute to the univariate free Malliavin-Stein method. Secondly, we will use the notion of Free Stein kernel introduced by M.Fathi and B.Nelson in 2017, as well as free functional inequalities to obtain multivariate extensions of these results. In particular, we will provide quantitative bounds for the (non-commutative) Wasserstein distance between self-adjoint vector-valued Wigner integrals and semicircular families with positive definite covariance matrix. This last result can be seen as a (weaker) non-commutative counterpart of the famous theorem of I.Nourdin, G.Peccati and A.Revéillac which estimates the Wasserstein distance between a vector of Malliavin differentiable random variables and a gaussian vector with positive definite covariance matrix. And finally, we will provide several examples of applications, such as the rate of convergence in the multivariate free Breuer-Major CLT for the free fractional Brownian motion.

Abstract: The most known example of a class of non-Gaussian stochastic processes which belongs to the homogeneous Wiener chaos of an arbitrary order N > 1 are probably Hermite processes of rank N. They generalize fractional Brownian motion (fBm) and Rosenblatt process in a natural way. They were introduced several decades ago. Yet, in contrast with fBm and many other Gaussian and stable stochastic processes and fields related to it, few results on path behavior of Hermite processes are available in the literature. The goal of our talk is to derive a quasi-optimal lower bound for the asymptotic behavior of local oscillations of paths of Hermite processes of any rank N.

Abstract: In this talk I will provide a gentle introduction to the growing world of sport analytics. After talking about its genesis and giving some striking examples from professional sports, I will describe how one can use probability distributions to model the outcomes of football matches, and how this can be combined with machine learning procedures to predict big tournaments and hereby even outperform bookmakers. I will conclude with an outlook on how these findings can be translated to sports medicine and, in particular, the estimation of injury risks.

Abstract: We show the equivalence between the modified log-Sobolev inequality and a family of Beckner inequalities in the context of general Markov processes. As a consequence, we deduce that moment estimates implied by the modified log-Sobolev inequality are of the same form as those implied by the usual log-Sobolev inequality. We illustrate our findings with applications to the Poisson space.

Abstract: One of the most classical problems in multivariate statistics is considered, namely, the problem of testing isotropy, or equivalently, the problem of testing uniformity on the unit hypersphere. Rather than restricting to tests that can detect specific types of alternatives only, we consider the broad class of Sobolev tests. While these tests are known to allow for omnibus testing of uniformity, their non-null behavior and consistency rates, unexpectedly, remain largely unexplored. To improve on this, we thoroughly study the local asymptotic powers of Sobolev tests under the most classical alternatives to uniformity, namely, under rotationally symmetric alternatives. We show in particular that the consistency rate of Sobolev tests does not only depend on the coefficients defining these tests but also on the derivatives of the underlying angular function at zero.

Abstract: I’ll present two problems where data naturally present a graphical structure: the analysis of champions in a tournament and the problem of matching. I’ll present for each problem intuitive results in toy models and discuss various mathematical tools involved to prove them. I’ll also present many open problems, hopefully convincing people to jump in this growing area.

Abstract: A standard way to move particles in a SMC sampler is to apply several steps of a MCMC (Markov chain Monte Carlo) kernel. Unfortunately, it is not clear how many steps need to be performed for optimal performance. In addition, the output of the intermediate steps are  discarded and thus wasted somehow. We propose a new, waste-free SMC algorithm which uses the outputs of all these intermediate MCMC steps as particles. We establish that its output is consistent and asymptotically normal. We use the expression of the asymptotic variance to develop various insights on how to implement the algorithm in practice. We develop in particular a method to estimate, from a single run of the algorithm, the asymptotic variance of any particle estimate. We show empirically, through a range of numerical examples, that waste-free SMC tends to outperform standard SMC samplers, and especially so in situations where the mixing of the considered MCMC kernels decreases across iterations (as in tempering or rare event problems).

Abstract: Hypothesis testing in high dimensions has been a most active research topics in the last decade. Both theoretical and practical considerations make it natural to restrict to sign tests, that is, to tests that uses observations only through their directions from a given center. This obviously maps the original Euclidean problem to a spherical one, still in high dimensions. With this motivation in mind, we tackle two testing problems on high-dimensional spheres, both under a symmetry assumption that specifies that the distribution at hand is invariant under rotations with respect to a given axis. More precisely, we consider the problem of testing the null hypothesis of uniformity (“detecting the signal”) and the problem of testing the null hypothesis that the symmetry axis coincides with a given direction (“learning the signal direction”). We solve both problems by exploiting Le Cam’s asymptotic theory of statistical experiments, in a double- or triple-asymptotic framework. Interestingly, contiguity rates depend in a subtle way on how well the parameters involved are identified as well as on a possible further antipodally-symmetric nature of the distribution. In many cases, strong optimality results are obtained from local asymptotic normality. When this cannot be achieved, it is still possible to establish minimax rate optimality.

Abstract: Independence measures based on Reproducing Kernel Hilbert Spaces, also known as Hilbert-Schmidt Independence Criterion and denoted HSIC, are widely used to statistically decide whether or not two random vectors are dependent since the seminal work by [Gretton et al., 2005]. Non-parametric HSIC-based statistical tests of independence have been performed, see [Gretton et al., 2008]. However, these tests lead to the question of the choice of the kernels associated to the HSIC. In particular, there is as yet no method to objectively select specific kernels with theoretical guarantees in terms of first and second kind errors. One of the main contributions of this work is to develop a new HSIC-based aggregated procedure which avoids such a kernel choice, and to provide theoretical guarantees for this procedure. To achieve this, we first introduce non-asymptotic single tests based on Gaussian kernels with a given bandwidth, which are of prescribed level α ∈ (0, 1). From a theoretical point of view, we upper-bound their uniform separation rate of testing over Sobolev and Nikol’skii balls. The key tools to obtain the theoretical performances of the test are exponential inequalities for U-statistics due to [Arcones and Giné, 1993] and [Giné et al., 2000]. Then, we aggregate several single tests, and obtain similar upper-bounds for the uniform separation rate of the aggregated procedure over the same regularity spaces. Another main contribution is that we provide a lower-bound for the non-asymptotic minimax separation rate of testing over Sobolev balls, and deduce that the aggregated procedure is adaptive in the minimax sense over such regularity spaces. The non-asymptotic lower bound is based on the work by [Baraud, 2002]. Finally, from a practical point of view, we perform numerical studies in order to assess the efficiency of our aggregated procedure and compare it to existing independence tests in the literature, in particular to the statistical test of independence based on the kernel mutual information recently studied by [Berrett and Samworth, 2017]. The paper is available on Hal [Albert et al., 2020].

Abstract: In this talk we will give an exact characterization for the asymptotic distribution of quadratic forms in IID random variables with finite second moment, where the underlying matrix is the adjacency matrix of a graph. In particular we will show that the limit distribution of such a quadratic form can always be expressed as the sum of three independent components: a Gaussian, a (possibly) infinite sum of centered chi-squares, and a Gaussian with a random variance. As a consequence, we derive necessary and sufficient conditions for asymptotic normality, and universality of the limiting distribution.

Abstract: In this work we undertake a thorough study of the non-asymptotic properties of the vanilla generative adversarial networks (GANs). We derive theoretical guarantees for the density estimation with GANs under a proper choice of the deep neural networks classes representing generators and discriminators. In particular, we prove that the resulting estimate converges to the true density in terms of Jensen-Shannon (JS) divergence at the rat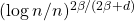e where 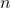is the sample size and 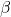determines the smoothness of . To the best of our knowledge, this is the first result in the literature on density estimation using vanilla GANs with JS convergence rates faster than 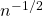in the regime 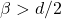. Moreover, we show that the obtained rate is minimax optimal for the considered class of densities.

Abstract: We discuss an approach to estimate aggregation and adaptive estimation based upon (nearly optimal) testing of convex hypotheses. We show that in the situation where the observations stem from simple observation schemes (i.e, have Gaussian, discrete and Poisson distribution) and where the set of unknown signals is a finite union of convex and compact sets, the proposed approach leads to aggregation and adaptation routines with nearly optimal performance. As an illustration, we consider application of the proposed estimates to the problem of recovery of unknown signal known to belong to a union of (sic) in Gaussian observation scheme. The corresponding numerical routines can be implemented efficiently when the number of sets in the union is “not very large”. We illustrate the “practical performance” of the method in a numerical example of estimation in the single index model.

Abstract: I consider the deconvolution problem in the case where no information is known about the noise distribution. More precisely, no assumption is made on the noise distribution and no samples are available to estimate it: the deconvolution problem is solved based only on observations of the corrupted signal. I will prove the identifiability of the model up to translation when the signal has a Laplace transform with an exponential growth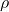 smaller than 2 and when it can be decomposed into two dependent components, so that the identifiability theorem can be used for sequences of dependent data or for sequences of iid multidimensional data.  In the case of iid multidimensional  data, I will propose an adaptive estimator of the density of the signal and provide rates of convergence. This rate of convergence is known to be minimax when ρ = 1.